Smartphone Usage Statistics By Users, Usage, Penetration, Activities, Addiction and Future Predictions
Updated · Jul 02, 2025

Table of Contents
- Introduction
- Editors Choice
- Global Key Figures
- Regional Key Figures
- General Smartphone Usage Statistics
- Smartphone Users In India
- Parents’ And Teens’ Smartphone Usage And Addiction Statistics
- Smartphone Usage By Global
- Share Of Smartphone Users In United Kingdom Statistics
- Global Number Of Smartphone Users Statistics
- Smartphone Penetration Statistics
- Activities Done By My Smartphone Users Statistics
- Work Habits Influenced By Smartphone Addiction
- Smartphone Addiction And Reliance Statistics
- Most Used Smartphone Applications
- Future Prediction And Trends Of Smartphone Usage
- Conclusion
Introduction
Smartphone Usage Statistics: Smartphones have become a vital part of everyday life, especially in developed countries, where about 75% of people have one. Worldwide, smartphones make up nearly 90% of all mobile phones, with over 7.2 billion smartphones in use as of 2024. This growth shows no signs of stopping, as the smartphone market grew by 7.8% in the first quarter of 2024.
By the end of 2023, around 70% of the global population owned a smartphone. Many people have more than one device, pushing smartphone subscriptions past 7 billion. It’s expected that this number could reach nearly 8 billion by 2028, showing that smartphones are still in high demand and important in our daily lives. We shall shed light on Smartphone Usage Statistics through this article.
Editors Choice
- Nearly 45% of students say they are online all the time, even during class.
- 49% of students report being distracted by their phones, and 20% use them for non-academic activities in class.
- Nearly 47% of parents believe their kids are addicted to their devices.
- Smartphones were the second most popular electronic device in 2022. That year, 53% of Americans reported never being without their smartphones for more than 24 hours.
- In 2023, 93% of college graduates in the US owned a smartphone.
- In 2023, around 2 billion internet users use the web using smartphones, making up 58.14% of all internet users.
- Smartphone Usage Statistics stated that among users aged 18-34 in 2021, 58% chose an iPhone.
- Some individuals completely turn off their devices to stay focused, as they don’t trust themselves to concentrate with their phones on.
- As of January 2023, Apple iPhones made up 27.6% of the global smartphone market.
- In 2022, about 1.747 billion smartphones were sold worldwide, with the iPhone 12 being the best-selling model that year.
- In 2022, 25% of internet users shopped online using their smartphones.
- Samsung was the top smartphone seller in Africa as of 2023, according to Smartphone Usage Statistics.
- Recent data shows that France has the highest smartphone penetration rate, with 83.6% of the population owning a smartphone.
- In 2023, roughly 6.92 billion people, or 85.74% of the global population, owned smartphones.
- This number should rise to 7.13 billion by 2024, and by 2025, about 90.33% of the global population will own smartphones, totaling around 7.33 billion users.
Global Key Figures
-
Mobile Subscription
| Mobile subscription | 2022 | 2023 | Forecast 2029 | CAGR 2023-2029 | Unit |
| Global smartphone subscription | 8,320 | 8,500 | 9,260 | 1% |
million |
|
Fixed wireless access connections |
107 | 131 | 330 | 17% | million |
| Mobile subscriptions, 5G | 1,00 | 1,580 | 5,560 | 23% |
million |
|
Mobile subscriptions, WCDMA/HSPA |
850 | 570 | 290 | -13% | million |
| Mobile subscriptions, LTE | 5,290 | 5,210 | 3,010 | -9% |
million |
|
Mobile subscriptions, GSM/EDGE-only |
1,160 | 1,010 | 380 | -15% | million |
| Mobile broadband subscriptions | 7,050 | 7,390 | 8,820 | 3% |
million |
|
Mobile PC, tablet and mobile router subscriptions |
230 | 260 | 490 | 12% | million |
| Smartphone subscriptions | 6,570 | 6,930 | 8,100 | 3% |
million |
| Fixed broadband connection | 1,450 | 1,530 | 1,850 | 3% | million |
-
Mobile Data Traffic
| Mobile data traffic | 2022 | 2023 | Forecast 2029 | CAGR 2023-2029 | Unit |
| Data traffic per tablet | 11 | 14 | 32 | 16% | GB/month |
| Data traffic per mobile PC | 19 | 22 | 34 | 8% | GB/month |
| Data traffic per smartphone | 15 | 17 | 42 | 16% | GB/month |
-
Total Data Traffic
| Total data traffic | 2022 | 2023 | Forecast 2029 | CAGR 2023-2029 | Unit |
| Mobile data traffic | 88 | 106 | 313 | 20% | EB/month |
| 1]Tablets | 0.7 | 0.9 | 2.7 | 21% | EB/month |
| 2]Mobile PCs and routers | 0.8 | 1 | 2.4 | 17% | EB/month |
| 3]Smartphones | 87 | 104 | 307 | 20% | EB/month |
| Fixed wireless access | 22 | 30 | 154 | 31% | EB/month |
| Total mobile network traffic | 110 | 137 | 466 | 23% | EB/month |
| Total fixed data traffic | 270 | 330 | 660 | 12% | EB/month |
Regional Key Figures
-
Mobile Subscription
| Mobile subscriptions | 2022 | 2023 | Forecast 2029 | CAGR[3] 2023–2029 |
Unit |
| Gulf Cooperation Council (GCC)[2] | 75 | 77 | 91 | 3% | million |
| Sub-Saharan Africa | 900 | 950 | 1,170 | 4% | million |
| India, Nepal and Bhutan | 1,150 | 1,180 | 1,290 | 1% | million |
| Middle East and North Africa | 730 | 730 | 830 | 2% | million |
| North-East Asia | 2,160 | 2,200 | 2,290 | 1% | million |
| China[1] | 1,690 | 1,730 | 1,790 | 1% | million |
| South East Asia and Oceania | 1,140 | 1,160 | 1,300 | 2% | million |
| Latin America | 710 | 720 | 780 | 1% | million |
| Western Europe | 540 | 550 | 560 | 0% | million |
| Central and Eastern Europe | 560 | 560 | 560 | 0% | million |
| North America | 430 | 440 | 480 | 2% | million |
-
Smartphone Subscription
| Smartphone subscriptions | 2022 | 2023 | Forecast 2029 | CAGR[3] 2023–2029 |
Unit |
| GCC | 63 | 66 | 80 | 3% | million |
| Sub-Saharan Africa | 420 | 460 | 790 | 9% | million |
| India, Nepal and Bhutan | 810 | 880 | 1,200 | 5% | million |
| Middle East and North Africa | 560 | 640 | 750 | 2% | million |
| North-East Asia | 2,020 | 2,070 | 2,180 | 1% | million |
| China[1] | 1,600 | 1,640 | 1,720 | 1% | million |
| South East Asia and Oceania | 950 | 970 | 1,150 | 3% | million |
| Latin America | 570 | 600 | 690 | 3% | million |
| Western Europe | 470 | 480 | 490 | 0% | million |
| Central and Eastern Europe | 410 | 450 | 450 | 0% | million |
| North America | 360 | 380 | 400 | 1% | million |
-
LTE Subscription
| LTE subscriptions | 2022 | 2023 | Forecast 2029 | CAGR 2023–2029 |
Unit |
| GCC | 55 | 46 | 6 | -29% | million |
| Sub-Saharan Africa | 267 | 330 | 440 | 5% | Million |
| India, Nepal and Bhutan | 780 | 740 | 410 | -9% | million |
| Middle East and North Africa | 420 | 470 | 380 | -3% | million |
| North-East Asia | 1,400 | 1,220 | 440 | -16% | million |
| China | 1,050 | 890 | 260 | -18% | million |
| South East Asia and Oceania | 840 | 910 | 640 | -6% | million |
| Latin America | 520 | 530 | 280 | -10% | million |
| Western Europe | 430 | 380 | 80 | -23% | million |
| Central and Eastern Europe | 410 | 460 | 280 | -8% | million |
| North America | 240 | 170 | 50 | -19% | million |
-
5G Subscription
| 5G subscriptions | 2022 | 2023 | Forecast 2029 | CAGR 2023–2029 |
Unit |
| Sub-Saharan Africa | 3 | 11 | 320 | N/A | million |
| GCC | 13 | 26 | 81 | 21% | million |
| Middle East and North Africa | 18 | 36 | 420 | N/A | million |
| China[1] | 569 | 771 | 1,500 | 12% | million |
| South East Asia and Oceania | 33 | 61 | 560 | N/A | million |
| India, Nepal and Bhutan | 10 | 119 | 840 | N/A | million |
| Central and Eastern Europe | 6 | 14 | 280 | N/A | million |
| North-East Asia | 674 | 908 | 1,820 | 12% | million |
| Latin America | 10 | 33 | 400 | N/A | million |
| Western Europe | 72 | 143 | 480 | 22% | million |
| North America | 173 | 257 | 430 | 9% | million |
-
Data traffic per smartphone
| Data traffic per smartphone | 2022 | 2023 | Forecast 2029 | CAGR 2023–2029 |
Unit |
| Sub-Saharan Africa | 3.7 | 5 | 20 | 26% | GB/month |
| GCC | 24 | 28 | 58 | 13% | GB/month |
| India, Nepal and Bhutan | 26 | 29 | 68 | 15% | GB/month |
| Middle East and North Africa | 12 | 14 | 43 | 20% | GB/month |
| North-East Asia | 17 | 19 | 41 | 14% | GB/month |
| China | 17 | 19 | 41 | 13% | GB/month |
| South East Asia and Oceania | 14 | 17 | 42 | 16% | GB/month |
| Western Europe | 17 | 19 | 49 | 17% | GB/month |
| Central and Eastern Europe | 14 | 17 | 43 | 17% | GB/month |
| North America | 17 | 19 | 59 | 21% | GB/month |
| Latin America | 9.3 | 11 | 36 | 22% | GB/month |
-
Total Mobile data traffic
| Total mobile data traffic | 2022 | 2023 | Forecast 2029 | CAGR 2023–2029 |
Unit |
| Sub-Saharan Africa | 1.4 | 2 | 13 | 38% | EB/month |
| GCC | 1.2 | 1.5 | 3.7 | 17% | EB/month |
| India, Nepal and Bhutan | 17 | 21 | 67 | 21% | EB/month |
| Middle East and North Africa | 5.9 | 7.9 | 28 | 24% | EB/month |
| China[1] | 25 | 29 | 65 | 15% | EB/month |
| South East Asia and Oceania | 12 | 15 | 44 | 20% | EB/month |
| Central and Eastern Europe | 4.5 | 5.8 | 15 | 17% | EB/month |
| North-East Asia | 29 | 33 | 78 | 15% | EB/month |
| Latin America | 4.6 | 5.8 | 22 | 25% | EB/month |
| Western Europe | 7 | 8.3 | 22 | 17% | EB/month |
| North America | 6.3 | 7.4 | 24 | 22% | EB/month |
General Smartphone Usage Statistics
- There are about 6.94 billion cell phones in use around the globe per Smartphone Usage Statistics.
- The count of cell phone users has increased by almost 6% each year for the last five years.
- By 2024, it’s expected that the number of cell phone users worldwide will reach 8.1 billion.
- China is the nation with the most smartphone users, while Germany has huge smartphone use per person.
- Almost 91% of university graduates have a smartphone, and Android is a very famous, widely used MOS.
- In 2023, roughly 7.92 billion people, or 86.74% of the worldwide people, owned cell phones.
- This number should rise to 7.14 billion by 2024, and by 2025, about 91.33% of the worldwide population will own cell phones, totaling around 7.34 billion users.
 (Reference: zippia.com)
(Reference: zippia.com)
- The total count of cell phone users is expected to hit 7.92 billion by 2028, marking fifteen straight years of growth.
- The estimate for 2026 is about 7.52 billion smartphone users.
- In 2023, around 2 billion internet users use the web using smartphones, making up 58.14% of all internet users.
Smartphone Users In India
 (Source: statista.com)
(Source: statista.com)
- In 2023, it was estimated that India had over one billion smartphone users. By 2040, this number is expected to grow to 1.55 billion.
- Globally, the number of smartphone users is projected to reach nearly 7.7 billion by 2027.
- By 2022, it was expected that more than two-thirds of the world’s population would use a smartphone.
- China has quickly become the leader in the smartphone market, leaving the US far behind.
- In 2023, about 72% of Chinese people used smartphones, and this number is projected to rise to over 83% by 2028.
- In 2023, there were nearly 1.04 billion smartphone users in China, as per Smartphone Usage Statistics.
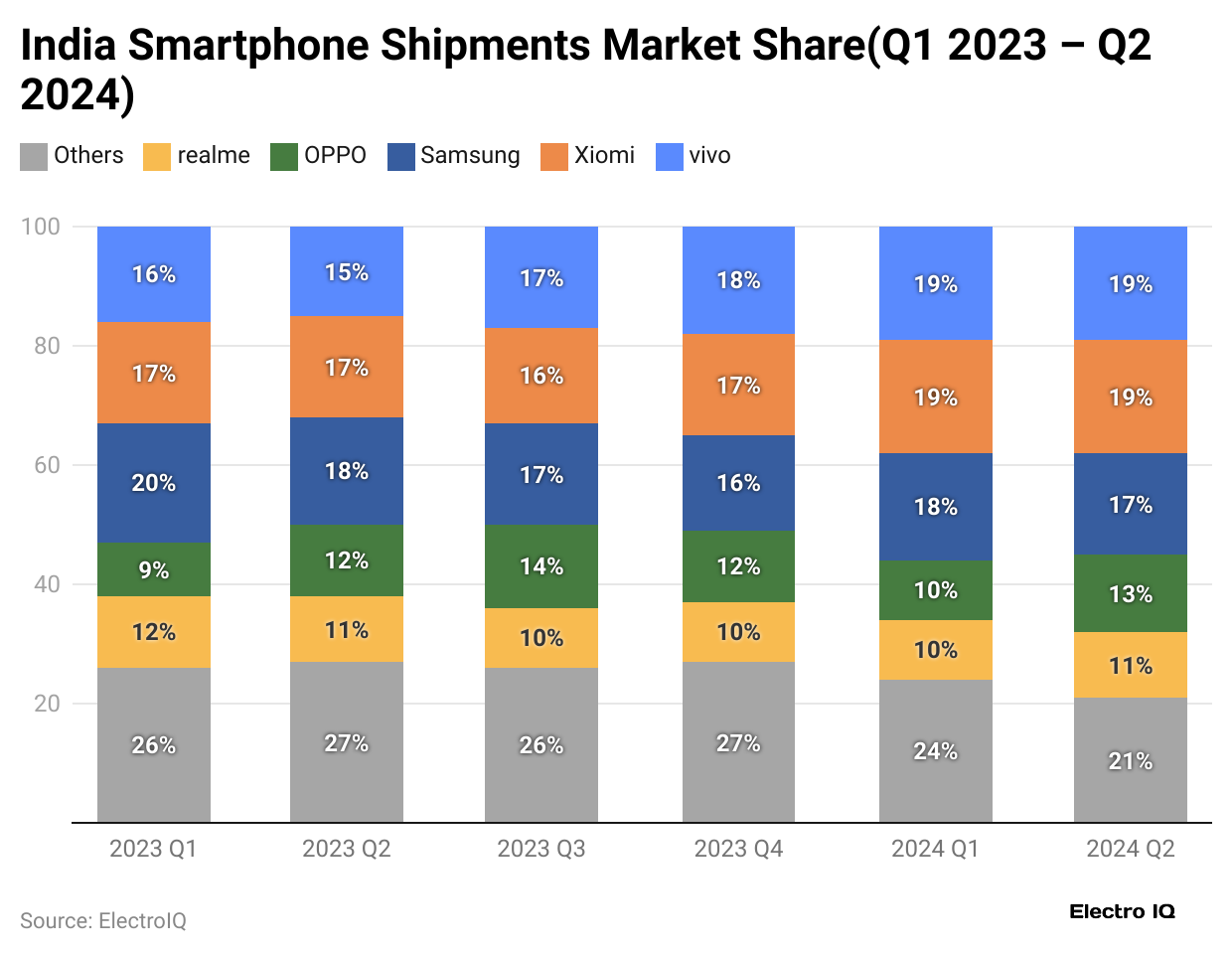
- India, the second most populated country, surpassed the US in smartphone users in 2017, with around 340 million users compared to 223 million in the US.
- Even with more users, the US still has a higher smartphone penetration rate. By 2023, India’s smartphone penetration rate was close to 71%, while the US reached this rate in 2019.
- In 2023, Samsung was the leading smartphone brand in India, followed by Xiaomi and Vivo.
Parents’ And Teens’ Smartphone Usage And Addiction Statistics
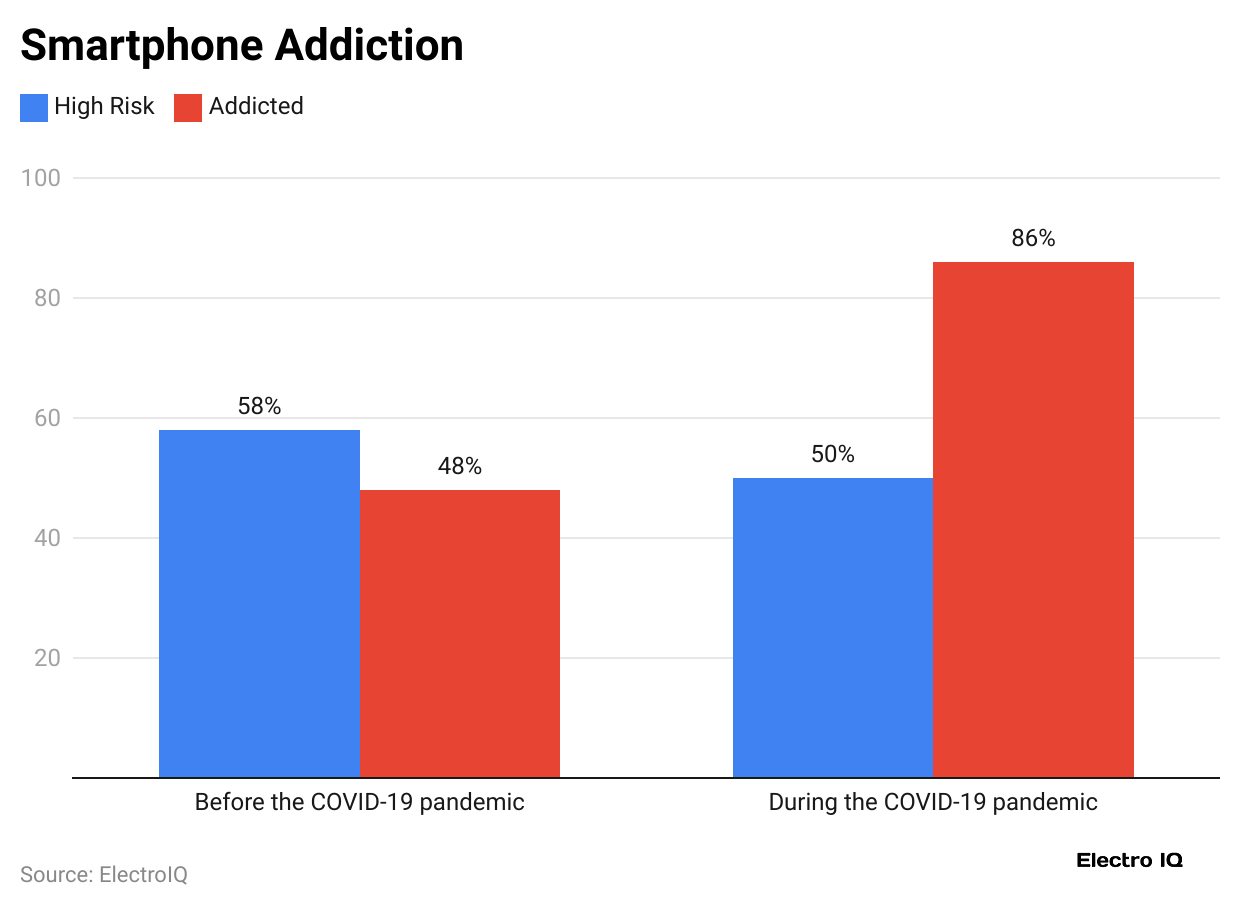
- Teens who use electronic devices for five or more hours a day are 71% more likely to show signs of suicide risk compared to those who use them for only one hour daily. Additionally, 47% of parents think their child may be addicted to smartphones.
- Among teachers surveyed, 67% noticed that students often get negatively distracted by their mobile devices.
- Meanwhile, 89% of parents feel responsible for overseeing their child’s cell phone use.
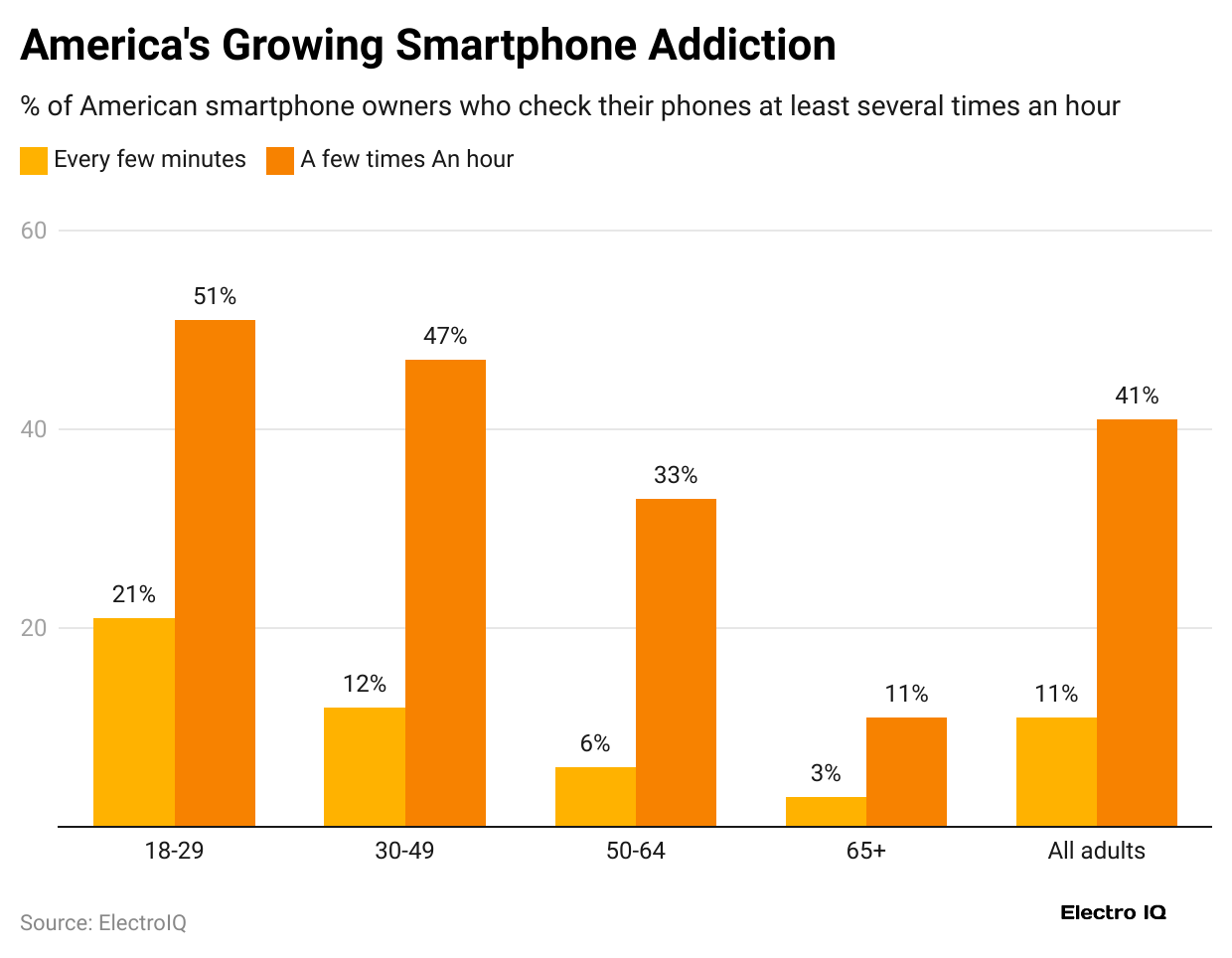
- In the 18- to 29-year-old age group, 22% of smartphone users said they check their phones every few minutes, suggesting possible addiction.
- About 36% of millennials reported spending two or more hours each workday on their phones for social media, texting, playing games, and engaging with marketing messages.
- A significant 41% of teens feel overwhelmed by the number of text alerts they receive each day, and 85% find it hard to stop using technology like the internet and smartphones once they start.
- Additionally, 67% of teens said they lose sleep because of late-night phone or internet use.
 (Reference: biomedcentral.com)
(Reference: biomedcentral.com)
- In the UK, 46% of parents said they “feel addicted” to their mobile devices. Instead of meeting in person, 33% of teens spend more time socializing with friends online.
- Also, 52% of teens reported sitting quietly on their smartphones for long periods while hanging out with friends.
- When it comes to smartphone and cell phone usage by country, China leads, followed by India and then the United States.
- As of 2024, 97% of American adults own a cell phone, and most reply to texts within minutes.
- About one in five American adults are “smartphone-only” internet users, meaning they use a smartphone but don’t have traditional home internet.
- Additionally, 48% of people feel anxious when their phone battery goes below 20%. This fear is known as nomophobia, which means the fear of being disconnected.
- On average, Americans look at their phones for 4 hours and 37 minutes each day. A typical smartphone user interacts with their device—by clicking, tapping, or swiping—about 2,617 times a day.
- Half of the people surveyed feel uneasy if they forget their phones at home.
- Smartphone Usage Statistics stated that Cell phone use while driving is responsible for 26% of car accidents.
- Among Americans aged 18 to 40, 47% are worried about how their phone usage affects their emotional health, while 51% are concerned about its effect on their physical health.
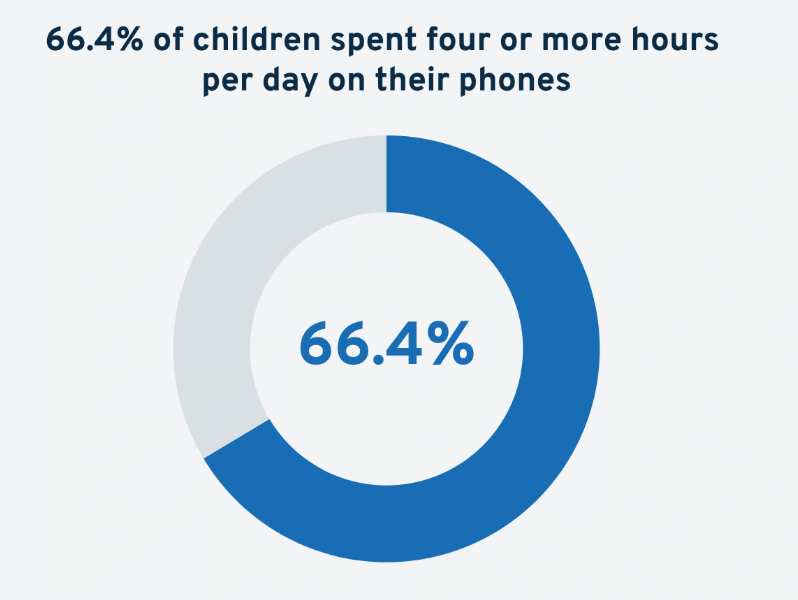 (Source: niagararecovery.com)
(Source: niagararecovery.com)
- Moreover, 56% believe that using their phones less would make their partner happier.
- Many people silence their phones or turn off notifications to reduce phone distractions, but a Penn State study found that this can lead to checking phones more often.
- Additionally, 87% of smartphone users check their devices within an hour of going to sleep or waking up, and 69% do so within the first five minutes of waking up.
- Interestingly, there are now more smartphones in the world than toilets.
Smartphone Usage By Global
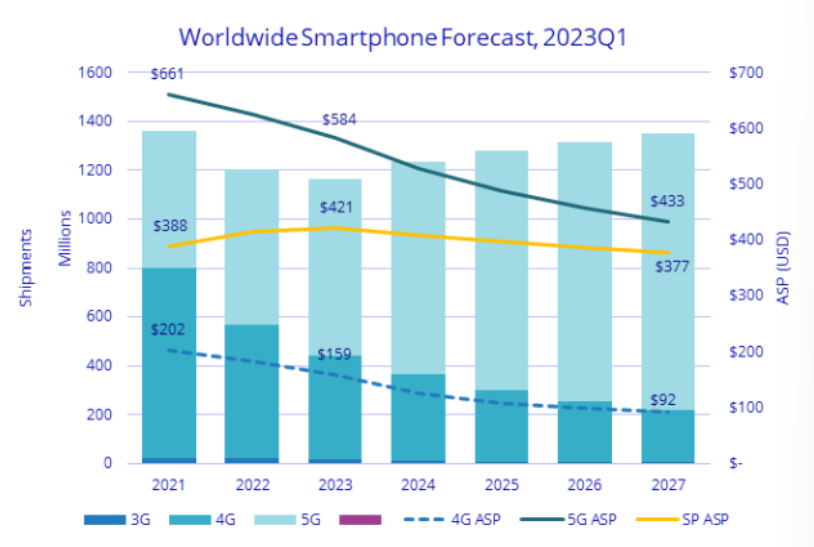
- In the Q1of 2023, the worldwide smartphone industry shares were as follows: Samsung at 23%, Apple at 23%, Xiaomi at 12%, OPPO at 13%, Vivo at 9%, and other brands at 29%.
- By the third quarter, Samsung and Apple both held 20% and 16%, respectively. Xiaomi and OPPO each had 14%, Vivo had 7%, and other brands remained at 29%.
- Overall, the smartphone market saw a 1% decline from the previous year, with around 299.8 million units shipped in 2023.
- Despite an 8% drop from the year before, Samsung continued to be the top player, holding 11% of the market in the last quarter, according to Smartphone Usage Statistics.
- By April 2023, the revenue forecast from smartphone shipments was expected to be: 4G smartphones at $159 million, standard smartphones at $584 million, and 5G smartphones at $421 million.
- For 2027, the predicted revenue from smartphone shipments is expected to be $92 million for 4G smartphones, $377 million for standard smartphones, and $433 million for 5G smartphones.
 (Source: statista.com)
(Source: statista.com)
| Year | Aged 16-24 | Aged 25-34 | Aged 35-44 | Aged 45-54 | Aged 55-64 | Aged 65+ |
| 2012 | 86% | 75% | 71% | 46% | 9% | 3% |
| 2013 | 90% | 88% | 78% | 66% | 40% | 20% |
| 2014 | 84% | 88% | 84% | 74% | 49% | 26% |
| 2015 | 93% | 92% | 85% | 80% | 56% | 28% |
| 2016 | 93% | 90% | 86% | 85% | 59% | 39% |
| 2017 | 93% | 91% | 89% | 85% | 64% | 46% |
| 2018 | 96% | 98% | 94% | 87% | 71% | 55% |
| 2019 | 98% | 98% | 95% | 95% | 80% | 62% |
| 2020 | 98% | 98% | 98% | 95% | 87% | 65% |
| 2021 | 98% | 99% | 97% | 98% | 90% | 69% |
| 2022 | 100% | 97% | 97% | 97% | 89% | 67% |
| 2023 | 99% | 99% | 99% | 98% | 91% |
71% |
- Smartphone usage in the United Kingdom has grown among all age groups since 2012, particularly for those aged 55 to 64.
- In 2012, only 9% of mobile users in this age group had a smartphone, but by 2023, that number had increased to over 90%.
- Smartphones are becoming more common and affordable. The global average price of a smartphone fell from $336.80 in 2010 to $276.20 in 2015.
- However, estimates from 2019 predicted that the average price would rise again, reaching $317 by 2021.
- In Europe, the average smartphone price was about 373 euros in 2019, according to smartphone usage statistics.
- Smartphones act like multi-purpose tools, with their abilities shaped by both the technology in the devices and the creativity of app developers.
- In 2017, communication was the most popular way to use phones.
- However, 87% of users reported frequently using camera apps, 85% used web browser apps often, and 68% frequently used navigation apps.
Global Number Of Smartphone Users Statistics
 (Reference: oberlo.com)
(Reference: oberlo.com)
- Here are the estimated numbers of global smartphone users over the years:
| Year | Amount |
| 2029 | 6.38 million |
| 2028 | 6.22 million |
| 2027 | 6.01 million |
| 2026 | 5.65 million |
| 2025 | 5.28 million |
| 2024 | 4.88 million |
| 2023 | 4.25 million |
| 2022 | 3.62 million |
| 2021 | 3.1 million |
| 2020 | 2.67 million |
| 2019 | 2.27 million |
| 2018 | 1.94 million |
| 2017 | 1.66 million |
| 2016 | 1.43 million |
| 2015 | 1.22 million |
| 2014 |
1.01 million |
- The current numbers show that the count of cell phone users is increasing every year.
- It is estimated that there will be 4.89 billion smartphone users worldwide in 2024, a 14.10% increase from the previous year.
- This is also 3.88 billion more than in 2014, meaning the number has nearly quintupled in ten years.
- Cell Phones are now the most famous electrical gadget, with 98.6% of all internet users relying on them.
- Looking ahead, reports suggest that the count of worldwide cell phone users will go on to rise and is expected to reach 6.38 billion by 2029.
- With a worldwide population predicted to be almost 8.5 billion till then, the smartphone penetration rate will be around 75.2%. This means that more than three out of four people in the world will have a smartphone.
- The count of cellphones users is not evenly spread around various economies.
- As predicted, ownership of cell phones is much higher in advanced economies, such as most European nations and the US.
- Recent data shows that France has the highest smartphone penetration rate, with 83.6% of the population owning a smartphone.
- The UK follows closely at 82.2%, with Germany at 81.9% and the US at 81.6%. Japan gets out the top five with a rate of 78.6%.
- In contrast, smartphone usage is much lower in emerging economies. For example, only 67.6% of people in Brazil own a smartphone, and this number drops to 47.5% in India.
- According to Smartphone Usage Statistics, less than one in four people (30.4%) in Bangladesh use smartphones.
Smartphone Penetration Statistics
- Smartphone adoption varies by country and region. Here’s the latest information on smartphone penetration, highlighting the countries with the highest rates and total users.
- The United Kingdom has the highest smartphone penetration, with 82.20% of its population owning a smartphone, or about 54.70 million smartphone users.
 (Reference: broadbandsearch.com)
(Reference: broadbandsearch.com)
- China leads in the total number of smartphone users, with 782.8 million users. However, its market penetration is only 55.30% because China has a total population of 1.415 billion people.
- Following are the Top 20 Countries by Smartphone Penetration:
| Rank | Market/Countries | Total Population | Smartphone Penetration | Smartphone Users |
| 20 | Romania | 19.6M | 53.80% | 10.5M |
| 19 | Japan | 127.2M | 55.3% | 70.3M |
| 18 | China | 1,415.0 | 55.30% | 782.8M |
| 17 | Malaysia | 32.0M | 57.50% | 18.4M |
| 16 | Italy | 59.3M | 58.00% | 34.4M |
| 15 | Taiwan | 23.7M | 60.0% | 14.2M |
| 14 | Russian Federation | 144.0M | 63.80% | 91.9M |
| 13 | Poland | 38.1M | 64.00% | 24.4M |
| 12 | Kazakhstan | 18.4M | 64.90% | 11.9M |
| 11 | South Korea | 51.2M | 67.60% | 34.6M |
| 10 | Australia | 24.8M | 68.60% | 17.0M |
| 09 | Canada | 37.0M | 72.10% | 26.6M |
| 08 | Spain | 46.4M | 72.50% | 33.6M |
| 07 | France | 65.2M | 76.00% | 49.6M |
| 06 | Belgium | 11.5M | 76.60% | 8.8M |
| 05 | United States | 326.8M | 77.00% | 251.7M |
| 04 | Sweden | 10.0M | 78.80% | 7.9M |
| 03 | Germany | 82.3M | 78.80% | 64.8M |
| 02 | Netherlands | 17.1M | 79.30 | 13.5M |
| 01 | United Kingdom | 66.6M | 82.20% |
54.7M |
- Average Global Smartphone Penetration Statistics:
| Year | Number of Smartphone users(in billion) | Worldwide population (in billions) | Percentage of smartphone users worldwide |
| 2014 | 1.01 | 7.30 | 14% |
| 2015 | 1.22 | 7.38 | 16% |
| 2016 | 1.43 | 7.47 | 19% |
| 2017 | 1.66 | 7.56 | 22% |
| 2018 | 1.94 | 7.64 | 25% |
| 2019 | 2.27 | 7.73 | 29% |
| 2020 | 2.67 | 7.81 | 34% |
| 2021 | 3.10 | 7.88 | 39% |
| 2022 | 3.62 | 7.94 | 46% |
| 2023 | 4.25 | 8.01 | 53% |
| 2024 | 4.88 | 8.08 | 60% |
| 2025 | 5.28 | 8.18 | 64% |
| 2026 | 5.65 | 8.26 | 68% |
| 2027 | 6.01 | 8.34 | 72% |
| 2028 | 6.22 | 8.42 | 74% |
| 2029 | 6.38 | 8.50 | 75% |
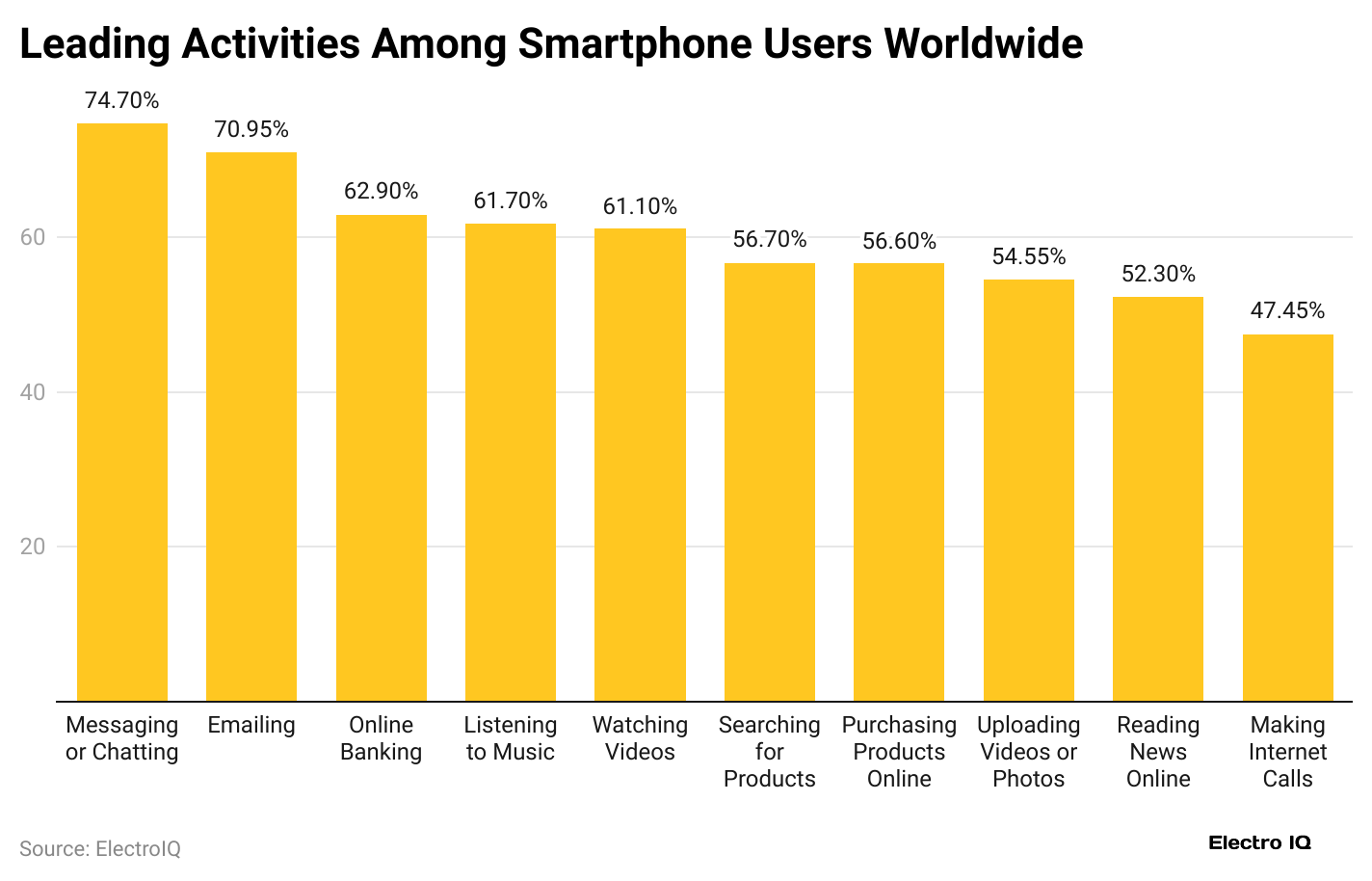
Activities Done By My Smartphone Users Statistics
- Nearly 83% of the population use cell phones to check emails and take photos.
- Almost 76% mainly use their cell phones to browse the internet.
- Smartphone Usage Statistics stated that almost 74% use them for maps.
- The report also uncovered more interesting results, which are explained down.
| Smartphone Actions | Share Of Respondents |
| Playing Games (Apps) | 52% |
| Watch long videos (Movies/TV) | 44% |
| Online Video Gaming | 35% |
| Taking Videos | 58% |
| Reading news | 58% |
| General purpose apps | 57% |
| Video Calls | 59% |
| Watch Short Videos (Clips/Messages) | 65% |
| Online Banking | 60% |
| Listening To Music/Podcasts | 66% |
| Maps/Directions | 73% |
| Online Shopping | 71% |
| Check/Post social media | 67% |
| Emails | 83% |
| Taking Photos | 83% |
| Surfing the Internet | 76% |
- Almost 78% of millennials in the US see videos on their cell phones around once a week.
- Roughly 64% regularly use social media.
- Around 62% listen to music on their cell phones.
- Smartphone Usage Statistics stated that nearly 57% play games.
Following are a few other popular cell phone actions that millennials enjoy:
| Smartphone Actions | Share Of Respondents |
| Online Investing | 13% |
| Get Sports News/Information | 12% |
| Online Dating | 5% |
| Get National News | 23% |
| Read Magazine Content | 19% |
| Read Newspaper Content | 16% |
| Research Products/Services to buy offline | 32% |
| Purchase Products or Services | 38% |
| Play Games | 54% |
| Research Products/Services to buy online | 44% |
| Get Weather Information | 43% |
| Do Online Banking | 40% |
| Get Local News | 32% |
| Watch Videos | 78% |
| Use social networks | 64% |
| Listen to Music | 62% |
- 42% of users in the US update their social media every day.
- According to Smartphone Usage Statistics, 45% of smartphone users make phone calls 1 to 4 times a day, while 30% reply to messages.
- Almost half of cell phone users click photos or record videos every day.
- 49% listen to music, audiobooks and podcasts each day.
- These numbers provide a clear view of how people use their smartphones.
| Smartphone Action | Once a Day | 1 to 3 times per day | 4 to 7 times per day | 8 to 10 times per day | More than ten times a day | Don’t know/No opinion | Smartphone Activities |
| Use GPS Navigation | 63% | 18% | 3% | 1% | 2% | 12% | Use GPS Navigation |
| Watch Movies, Television, or Other Video Content | 49% | 22% | 9% | 3% | 5% | 11% | Watch Movies, Television, or Other Video Content |
| Listen To Music, Podcasts, Audiobooks | 48% | 23% | 8% | 4% | 5% | 12% | Listen To Music, Podcasts, Audiobooks |
| Take Photos or Record Videos | 51% | 27% | 8% | 3% | 4% | 7% | Take Photos or Record Videos |
| Makes Phones Calls | 24% | 44% | 17% | 7% | 6% | 4% | Makes Phones Calls |
| Respond To Text Messages | 16% | 30% | 19% | 13% | 18% | 4% | Respond To Text Messages |
| Update Social Media | 43% | 27% | 10% | 5% | 6% | 9% | Update Social Media |
- These numbers show how people changed their smartphone usage during the pandemic.
Work Habits Influenced By Smartphone Addiction
- Distractions at work are everywhere, especially from smartphones. Many people struggle to focus because of notifications, which can pressure them to check their phones.
- Some individuals completely turn off their devices to stay focused, as they don’t trust themselves to concentrate with their phones on.
- In a survey, 59% of employees reported that smartphones are the biggest distractions at work, even more than other tools.
- Many get caught up in apps like TikTok and Instagram while trying to work, wasting a lot of time on simple tasks.
- Even though smartphones can be distracting, many people find them useful at work. Some use their phones to make calls to coworkers, do research, or calm themselves when they feel stressed.
- The issue of phone use during work isn’t just in the US; it’s also a concern in the UK. About 75% of workers there admit to using their phones while on the job.
- Smartphone addiction is a global problem, affecting millennials as well. Around 36% of millennials say they spend about 2 hours a day on their phones, often during work time.
- According to Smartphone Usage Statistics, many people see the harmful effects of smartphone addiction and want to reduce their time spent on their devices.
- Currently, 58% of smartphone users are trying to cut back, setting limits and goals to decrease their time on social media.
- While many think smartphone addiction only impacts Generation Z, it affects people of all ages.
- Some millennials spend more time on their phones than certain younger Gen Z users.
Smartphone Addiction And Reliance Statistics
Many smartphone users today show signs of nomophobia, which is the fear of being without their phones. This shows how deeply cell phones have become a part of our daily lives. Here are some worrying statistics that showcase our dependence on smartphones:
- Two thousand six hundred seventeen times: The average number of times users in the US touch their phones each day. For heavy users, this can extend 4,000 times.
- One hundred fifty times: On average, smartphone owners unlock their phones daily.
- Users check their phones approximately every 11 to 13 minutes.
- According to a study by Zippia, the average person checks their smartphone at least 96 times a day.
- 66% of smartphone users in the US check their smartphones up to 160 times a day, indicating a high level of addiction.
 (Reference: statista.com)
(Reference: statista.com)
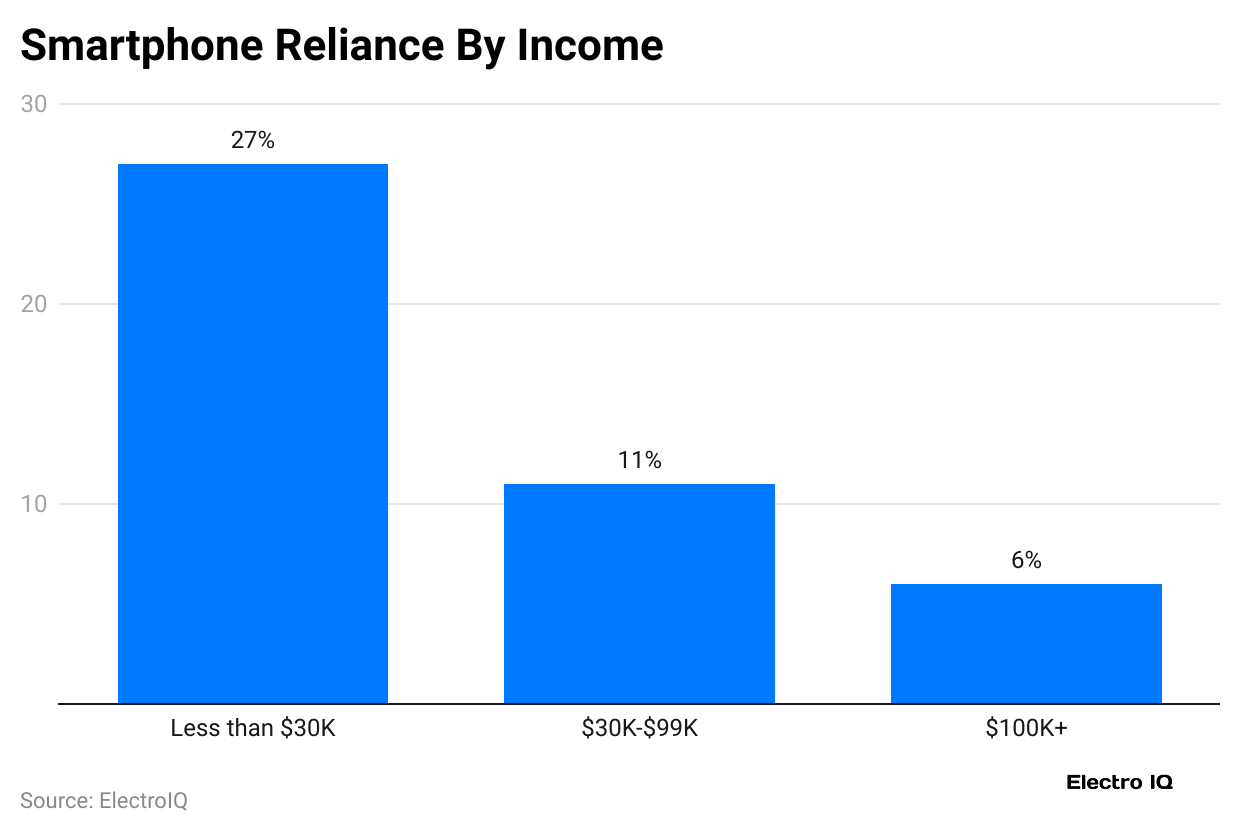
- Among those earning between $31,000 and $99,999, 11% rely on smartphones for internet access, which is related to 6% of individuals earning $100,000.
- 29% of people aged 18-29 have smartphones but need broadband internet.
- Only 12% of individuals aged 30-49 fall into this category, while 13% of those aged 50-64 and 12% of those over 66 do.
- 56% of teens feel alone, upset, or anxious without their phones.
- Smartphone Usage Statistics stated that almost 54% admit they spend too much time on their smartphones.
- 19% of teachers state smartphones distract students in school.
- Nearly 45% of people say they are online all the time, also during class.
- 49% of students report being distracted by their phones, and 20% use them for non-academic actions in class.
- Almost 21% of kids have cell phones by age 8.
- On average, Generation Z receives their first phone at 10.3 years old.
- 53% of kids in the US own a cell phone by the time they turn 11.
- 2% of smartphone users witness some level of nomophobia, with 37% having mild symptoms, 50% having moderate symptoms, and 13% having severe cases.
 (Reference: zippia.com)
(Reference: zippia.com)
- 88% of college kids and 66% of adults in the US report experiencing medium to severe nomophobia.
- Spending 5 hours or more on smartphones daily raises the risk of developing factors for suicide by 71% compared to those who use their devices for just an hour.
Most Used Smartphone Applications
- WhatsApp: With more than 2 billion active users, WhatsApp is the world’s most popular messaging app.
- Facebook: Even though it’s losing popularity among teens, Facebook still has over 2.8 billion monthly active users globally.
- YouTube: With over 2 billion monthly active users, YouTube is the second most popular search engine after Google.
- WeChat: This Chinese app has over 1.2 billion monthly active users and is used for messaging, social networking, and mobile payments.
- Instagram: With over 1 billion monthly active users, Instagram is the leading photo-sharing app worldwide.
- TikTok: The short video app has surged in popularity and now has over 689 million monthly active users.
- Snapchat: This app, known for disappearing messages, has over 500 million monthly active users around the world.
- Twitter: The microblogging site has over 330 million monthly active users and serves as a platform for news and discussions.
- Telegram: This secure messaging app, known for its end-to-end encryption, now has over 500 million monthly active users.
- Zoom: The video conferencing app became crucial for remote work during the COVID-19 pandemic, with over 300 million daily meeting participants.
Future Prediction And Trends Of Smartphone Usage
- Smartphone use is projected to grow by 2% to 3%, reaching about 7.34 billion users by 2025, according to Smartphone Usage Statistics.
- By 2027, it’s estimated there will be around 7.69 billion smartphone subscriptions.
- By 2025, about 72.6% of global smartphone owners are expected to access the internet only through their smartphones. Right now, there are roughly 10.37 billion mobile connections worldwide.
- In 2016, there were just 3.67 billion smartphone users, which made up 45% of the total population.
- As of 2023, that figure has jumped to 85% of the world’s population. Since 2016, the number of smartphone users worldwide has grown by 50%.
Conclusion
By looking at the rise of mobile shopping and how digital advertising has changed, you can better understand how customers are using their mobile devices and what the future may bring. These Mobile Usage Statistics can help you develop a mobile-first strategy to boost your dropshipping business.
This strategy can lead to higher engagement, more traffic, and, ultimately, increased sales. So, use this information to give your business a competitive advantage today!
Sources
FAQ.
64% of Americans Always Have Their Phones With Them. Most Americans keep their phones nearby all the time, and 80% of smartphone users check their phones within 15 minutes of waking up. A lot of people look at their phones right after getting out of bed.75% of People Admit to Using Their Phones During Work Meetings. Many people say they use their phones while in meetings at work, and 67% of people check their phones while talking to friends and family. A significant number of people look at their phones even when they are chatting with others.
Bloomberg data reveals that Bangladesh has the highest percentage of Android users at 98%. The global average is 83% and is still growing. Here are the countries with the most and the least Android smartphone users by region.
The AACAP recommends limiting non-educational screen time to one hour on weekdays and three hours on weekends for kids aged 2 to 5. For children 6 and older, there isn’t a specific hourly limit, but it’s advised to encourage healthy habits and reduce screen time activities.
Using devices too much can make you feel separated from friends and family. It can cause issues with concentration and learning. Always wanting to check your smartphone can distract you while you’re in class or at work. Plus, it usually means you’re less active physically.
Feeling upset or down after using your phone is quite common. Research shows that being too attached to smartphones can increase feelings of loneliness and depression, as well as harm your overall happiness. If you frequently feel bad after looking at your phone, it could mean that your phone use has become a concern.

Barry Elad is a tech enthusiast who loves diving deep into various technology topics. He gathers important statistics and facts to help others understand the tech world better. With a keen interest in software, Barry writes about its benefits and how it can improve our daily lives. In his spare time, he enjoys experimenting with healthy recipes, practicing yoga, meditating, or taking nature walks with his child. Barry’s goal is to make complex tech information easy and accessible for everyone.










